Nuair a thig e guantennaichean, is e a’ cheist as motha a tha a’ cur dragh air daoine “Ciamar a tha rèididheachd air a choileanadh dha-rìribh?” Ciamar a bhios an raon electromagnetic a chruthaicheas an stòr comharran a’ sgaoileadh tron loidhne tar-chuir agus taobh a-staigh an antenna, agus mu dheireadh a’ “sgaradh” bhon antenna gus tonn fànais shaor a chruthachadh.
1. Rèididheachd uèir singilte
Gabhamaid ris gu bheil an dùmhlachd cosgais, air a chur an cèill mar qv (Coulomb/m3), air a sgaoileadh gu cothromach ann an uèir chruinn le farsaingeachd earrann-tarsainn de a agus tomhas-lìonaidh de V, mar a chithear ann am Figear 1.
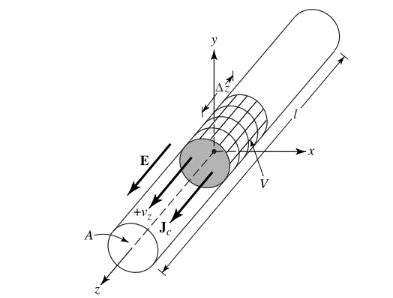
Figear 1
Bidh an cosgais iomlan Q ann an tomhas-lìonaidh V a’ gluasad ann an stiùireadh z aig astar cunbhalach Vz (m/s). Faodar a dhearbhadh gur e dùmhlachd an t-srutha Jz air earrann-tarsainn na uèire:
Jz = qv vz (1)
Ma tha an uèir air a dhèanamh de stiùiriche air leth freagarrach, is e dùmhlachd an t-sruth Js air uachdar na uèire:
Js = qs vz (2)
Far a bheil qs a’ riochdachadh dùmhlachd cosgais an uachdair. Ma tha an uèir glè thana (gu h-iomchaidh, is e 0 an radius), faodar an sruth san uèir a chur an cèill mar:
Iz = ql vz (3)
Far a bheil ql (coulomb/meatair) a’ riochdachadh a’ chosgais gach aonad faid.
Tha sinn gu sònraichte a’ dèiligeadh ri uèirichean tana, agus tha na co-dhùnaidhean a’ buntainn ris na trì cùisean gu h-àrd. Ma tha an sruth ag atharrachadh a rèir ùine, tha an t-atharrachadh de fhoirmle (3) a thaobh ùine mar a leanas:
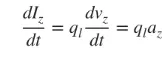
(4)
’S e az an luathachadh cosgais. Ma tha fad na uèire co-ionann ri l, faodar (4) a sgrìobhadh mar a leanas:
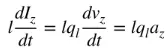
(5)
’S e co-aontar (5) am bun-cheangal eadar sruth agus cosgais, agus cuideachd am bun-cheangal eadar rèididheachd electromagnetic. Gu sìmplidh, gus rèididheachd a thoirt gu buil, feumaidh sruth no luathachadh (no lughdachadh) cosgais a bhith ann a bhios ag atharrachadh thar ùine. Mar as trice bidh sinn a’ toirt iomradh air sruth ann an tagraidhean co-sheirmeil thar ùine, agus is ann an tagraidhean sealach a thathas a’ toirt iomradh air cosgais as trice. Gus luathachadh (no lughdachadh) cosgais a thoirt gu buil, feumaidh an uèir a bhith lùbte, fillte, agus neo-leantainneach. Nuair a bhios an cosgais a’ crathadh ann an gluasad co-sheirmeil thar ùine, bheir e cuideachd luathachadh (no lughdachadh) cosgais bho àm gu àm no sruth a bhios ag atharrachadh thar ùine. Mar sin:
1) Mura gluais an cosgais, cha bhi sruth ann agus cha bhi rèididheachd ann.
2) Ma ghluaiseas an cosgais aig astar cunbhalach:
a. Mura h-eil rèididheachd ann, tha an uèir dìreach agus gun chrìoch a dh'fhaid.
b. Ma tha an uèir lùbte, fillte, no neo-leantainneach, mar a chithear ann am Figear 2, tha rèididheachd ann.
3) Ma bhios an cosgais ag atharrachadh thar ùine, bidh an cosgais a’ sgaoileadh eadhon ged a tha an uèir dìreach.
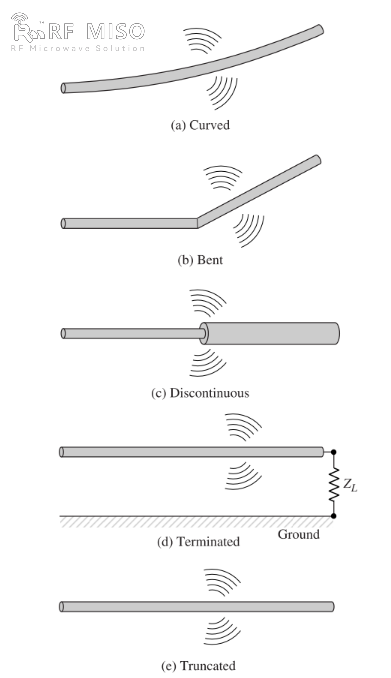
Figear 2
Gheibhear tuigse chàileachdail air meacanachd an rèididheachd le bhith a’ coimhead air stòr cuisleach ceangailte ri uèir fhosgailte a ghabhas talamh tro luchd aig a cheann fosgailte, mar a chithear ann am Figear 2(d). Nuair a thèid an uèir a chumhachdachadh an toiseach, bidh na cosgaisean (electronan saora) anns an uèir air an cur an gluasad leis na loidhnichean achaidh dealain a chruthaicheas an stòr. Mar a bhios na cosgaisean air an luathachadh aig ceann stòr na uèire agus air an slaodadh sìos (luathachadh àicheil an coimeas ris a’ ghluasad thùsail) nuair a thèid an nochdadh aig a cheann, bidh raon rèididheachd air a chruthachadh aig a cheann agus air feadh a’ chòrr den uèir. Tha luathachadh nan cosgaisean air a choileanadh le stòr feachd taobh a-muigh a chuireas na cosgaisean an gluasad agus a chruthaicheas an raon rèididheachd co-cheangailte. Tha lughdachadh nan cosgaisean aig cinn na uèir air a choileanadh le feachdan a-staigh co-cheangailte ris an raon brosnaichte, a tha air adhbhrachadh le cruinneachadh chosgaisean dùmhail aig cinn na uèire. Bidh na feachdan a-staigh a’ faighinn lùth bho chruinneachadh cosgais mar a bhios an astar aige a’ lùghdachadh gu neoni aig cinn na uèire. Mar sin, ’s e luathachadh nan cosgaisean mar thoradh air brosnachadh an raoin dealain agus lughdachadh nan cosgaisean mar thoradh air neo-leantainneachd no lùb rèidh bacadh na uèire na dòighean airson rèididheachd electromagnetic a chruthachadh. Ged a tha dùmhlachd an t-sruth (Jc) agus dùmhlachd cosgais (qv) le chèile nan teirmean tùsail ann an co-aontaran Maxwell, thathas den bheachd gu bheil cosgais na mheud nas bunaitiche, gu h-àraidh airson raointean sealach. Ged a thathas a’ cleachdadh an tuairisgeul seo air rèididheachd sa mhòr-chuid airson staidean sealach, faodar a chleachdadh cuideachd gus rèididheachd staid sheasmhach a mhìneachadh.
Molaibh grunn rudan sàr-mhathtoraidhean antennaair a dhèanamh leRFMISO:
2. Rèididheachd dà-uèir
Ceangail stòr bholtaids ri loidhne-tar-chuir dà-sheòladair ceangailte ri antenna, mar a chithear ann am Figear 3(a). Le bhith a’ cur bholtaids air an loidhne dà-uèir, bidh raon dealain ga chruthachadh eadar na sealadairean. Bidh na loidhnichean achaidh dealain ag obair air na dealanan saora (a tha furasta an sgaradh bho dadaman) a tha ceangailte ri gach sealadair agus gan toirt gu gluasad. Bidh gluasad nan cosgaisean a’ gineadh sruth, a bhios an uair sin a’ gineadh raon magnetach.
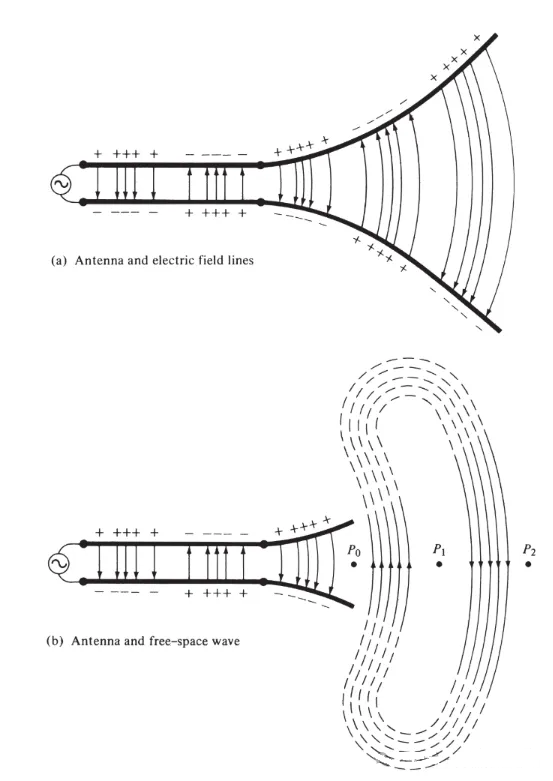
Figear 3
Tha sinn air gabhail ris gu bheil loidhnichean achaidh dealain a’ tòiseachadh le cosgaisean dearbhach agus a’ crìochnachadh le cosgaisean àicheil. Gu dearbh, faodaidh iad cuideachd tòiseachadh le cosgaisean dearbhach agus crìochnachadh aig neo-chrìochnach; no tòiseachadh aig neo-chrìochnach agus crìochnachadh le cosgaisean àicheil; no lùban dùinte a chruthachadh nach tòisich no nach crìochnachadh le cosgaisean sam bith. Bidh loidhnichean achaidh magnetach an-còmhnaidh a’ cruthachadh lùban dùinte timcheall air giùlan sruth oir chan eil cosgaisean magnetach ann am fiosaig. Ann an cuid de fhoirmlean matamataigeach, thèid cosgaisean magnetach co-ionann agus sruthan magnetach a thoirt a-steach gus an dà-chàirdeas eadar fuasglaidhean anns a bheil cumhachd agus stòran magnetach a shealltainn.
Bidh na loidhnichean achaidh dealain a tha air an tarraing eadar dà stiùiriche a’ cuideachadh le bhith a’ sealltainn mar a tha an cosgais air a sgaoileadh. Ma ghabhas sinn ris gu bheil an stòr bholtaids sinusoidal, tha sinn an dùil gum bi an raon dealain eadar na stiùirichean sinusoidal cuideachd le ùine co-ionann ri ùine an stòrais. Tha meud coimeasach neart an achaidh dealain air a riochdachadh le dùmhlachd nan loidhnichean achaidh dealain, agus tha na saigheadan a’ comharrachadh an stiùiridh coimeasach (deimhinneach no àicheil). Bidh gineadh raointean dealain is magnetach a bhios ag atharrachadh thar ùine eadar na stiùirichean a’ cruthachadh tonn electromagnetic a bhios a’ sgaoileadh air feadh na loidhne tar-chuir, mar a chithear ann am Figear 3(a). Bidh an tonn electromagnetic a’ dol a-steach don antenna leis a’ chosgais agus an t-sruth co-fhreagarrach. Ma bheir sinn air falbh pàirt de structar an antenna, mar a chithear ann am Figear 3(b), faodar tonn àite-saor a chruthachadh le bhith a’ “ceangal” cinn fosgailte nan loidhnichean achaidh dealain (air an sealltainn leis na loidhnichean dotaichte). Tha an tonn àite-saor cuideachd ùineil, ach bidh am puing ìre seasmhach P0 a’ gluasad a-mach aig astar solais agus a’ siubhal astar λ/2 (gu P1) ann an leth ùine. Faisg air an antenna, bidh am puing ìre-sheasmhach P0 a’ gluasad nas luaithe na astar an t-solais agus a’ tighinn faisg air astar an t-solais aig puingean fada bhon antenna. Tha Figear 4 a’ sealltainn sgaoileadh achaidh dealain an àite shaor den antenna λ∕2 aig t = 0, t/8, t/4, agus 3T/8.
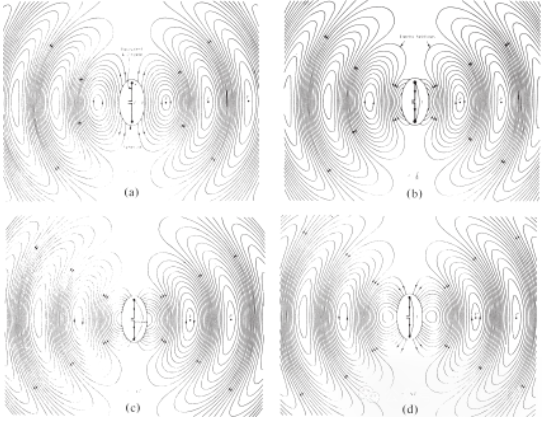
Figear 4 Sgaoileadh achaidh dealain àite shaor an antenna λ∕2 aig t = 0, t/8, t/4 agus 3T/8
Chan eil fios ciamar a tha na tonnan treòraichte air an sgaradh bhon antenna agus mu dheireadh air an cruthachadh gus sgaoileadh ann an àite saor. Is urrainn dhuinn tonnan treòraichte agus àite saor a choimeas ri tonnan uisge, a dh’ fhaodadh a bhith air adhbhrachadh le clach a thuiteas ann an uisge socair no ann an dòighean eile. Cho luath ‘s a thòisicheas an buaireadh san uisge, thèid tonnan uisge a chruthachadh agus tòisichidh iad a’ sgaoileadh a-mach. Fiù mura stad an buaireadh, chan eil na tonnan a’ stad ach a’ leantainn air adhart. Ma mhaireas an buaireadh, thèid tonnan ùra a chruthachadh gu cunbhalach, agus bidh sgaoileadh nan tonn sin a’ tuiteam às a chèile nan tonn eile.
Tha an aon rud fìor airson tonnan electromagnetic a thèid a chruthachadh le buaireadh dealain. Ma tha an buaireadh dealain tùsail bhon stòr goirid, bidh na tonnan electromagnetic a thèid a chruthachadh a’ sgaoileadh taobh a-staigh na loidhne tar-chuir, an uairsin a’ dol a-steach don antenna, agus mu dheireadh a’ rèididheachd mar thonnan àite saor, eadhon ged nach eil an brosnachadh an làthair tuilleadh (dìreach mar na tonnan uisge agus an buaireadh a chruthaich iad). Ma tha an buaireadh dealain leantainneach, bidh na tonnan electromagnetic ann gu leantainneach agus a’ leantainn gu dlùth air an cùlaibh rè sgaoileadh, mar a chithear san antenna dà-chònach a chithear ann am Figear 5. Nuair a tha tonnan electromagnetic taobh a-staigh loidhnichean tar-chuir agus antennas, tha an làthaireachd co-cheangailte ri làthaireachd cosgais dealain taobh a-staigh an t-seoltaiche. Ach, nuair a thèid na tonnan a rèididheachd, bidh iad a’ cruthachadh lùb dùinte agus chan eil cosgais ann gus an làthaireachd a chumail suas. Tha seo gar toirt chun cho-dhùnaidh:
Feumaidh brosnachadh an achaidh luathachadh agus lughdachadh a’ chìs, ach chan eil cumail suas an achaidh ag iarraidh luathachadh agus lughdachadh a’ chìs.
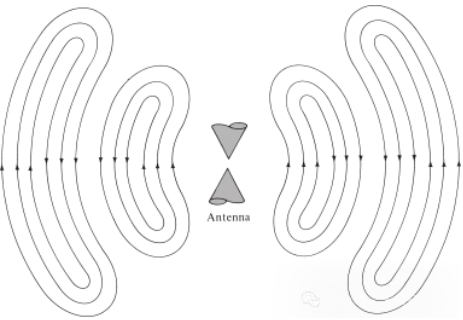
Figear 5
3. Rèididheachd dà-phòla
Bidh sinn a’ feuchainn ri mìneachadh a dhèanamh air an dòigh leis a bheil na loidhnichean achaidh dealain a’ briseadh air falbh bhon antenna agus a’ cruthachadh tonnan àite-saor, agus a’ gabhail an antenna dipole mar eisimpleir. Ged is e mìneachadh sìmplidh a th’ ann, tha e cuideachd a’ leigeil le daoine fhaicinn gu h-intuitive mar a chruthaichear tonnan àite-saor. Tha Figear 6(a) a’ sealltainn nan loidhnichean achaidh dealain a chaidh a chruthachadh eadar an dà ghàirdean den dipole nuair a ghluaiseas na loidhnichean achaidh dealain a-mach le λ∕4 anns a’ chiad chairteal den chearcall. Airson an eisimpleir seo, leig dhuinn gabhail ris gu bheil an àireamh de loidhnichean achaidh dealain a chaidh a chruthachadh 3. Anns an ath chairteal den chearcall, bidh na trì loidhnichean achaidh dealain tùsail a’ gluasad λ∕4 eile (iomlan de λ∕2 bhon àite tòiseachaidh), agus bidh dùmhlachd nan cosgaisean air an stiùiriche a’ tòiseachadh a’ lùghdachadh. Faodar a mheas mar a bhith air a chruthachadh le bhith a’ toirt a-steach cosgaisean mu choinneamh a chèile, a chuireas às do na cosgaisean air an stiùiriche aig deireadh a’ chiad leth den chearcall. Tha na loidhnichean achaidh dealain a chaidh a chruthachadh leis na cosgaisean mu choinneamh a chèile 3 agus bidh iad a’ gluasad astar λ∕4, a tha air a riochdachadh leis na loidhnichean dotaichte ann am Figear 6(b).
Is e an toradh deireannach gu bheil trì loidhnichean achaidh dealain sìos anns a’ chiad astar λ∕4 agus an aon àireamh de loidhnichean achaidh dealain suas anns an dàrna astar λ∕4. Leis nach eil cosgais lom air an antenna, feumar na loidhnichean achaidh dealain a sparradh gus dealachadh bhon stiùiriche agus tighinn còmhla gus lùb dùinte a chruthachadh. Tha seo air a shealltainn ann am Figear 6(c). Anns an dàrna leth, leanar an aon phròiseas fiosaigeach, ach thoir an aire gu bheil an stiùireadh mu choinneamh. Às deidh sin, ath-aithrisear am pròiseas agus leanaidh e gu bràth, a’ cruthachadh sgaoileadh achaidh dealain coltach ri Figear 4.
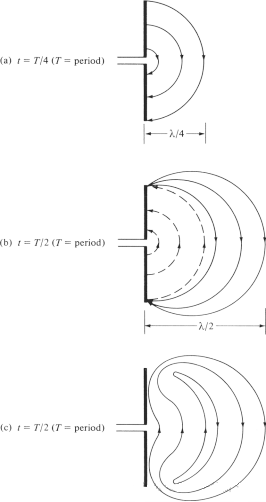
Figear 6
Gus barrachd ionnsachadh mu dheidhinn antennas, tadhail air:
Àm puist: Ògmhios-20-2024










